Tiệm cận là một khái niệm quan trọng trong toán học, đặc biệt là trong giải tích và hình học giải tích. Bạn đang tìm hiểu về tiệm cận và muốn nắm vững kiến thức này để đầu tư tiền điện tử hiệu quả hơn? Hãy cùng m5coin.com khám phá định nghĩa, cách tìm và ứng dụng của tiệm cận ngay sau đây để đưa ra những quyết định đầu tư sáng suốt.
1. Tiệm Cận Là Gì? Khái Niệm Cơ Bản Dành Cho Nhà Đầu Tư
Tiệm cận là một đường thẳng mà đồ thị của một hàm số tiến gần đến khi biến số (x) tiến đến một giá trị cụ thể (hữu hạn hoặc vô cùng). Nói một cách đơn giản, tiệm cận là “ranh giới” mà đồ thị hàm số “cố gắng” chạm tới nhưng không bao giờ thực sự cắt hoặc chạm vào. Hiểu rõ về tiệm cận giúp bạn phân tích đồ thị giá cả, dự đoán xu hướng và đưa ra quyết định đầu tư chính xác hơn.
Định nghĩa này có thể được hiểu rõ hơn khi xem xét các loại tiệm cận khác nhau, bao gồm tiệm cận đứng, tiệm cận ngang và tiệm cận xiên. Mỗi loại tiệm cận cung cấp một cái nhìn khác nhau về hành vi của hàm số và có thể được áp dụng trong nhiều lĩnh vực khác nhau, từ vật lý và kỹ thuật đến kinh tế và tài chính. Theo nghiên cứu của Đại học Stanford từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, việc hiểu rõ về tiệm cận cung cấp một công cụ mạnh mẽ để phân tích và dự đoán các hệ thống phức tạp.
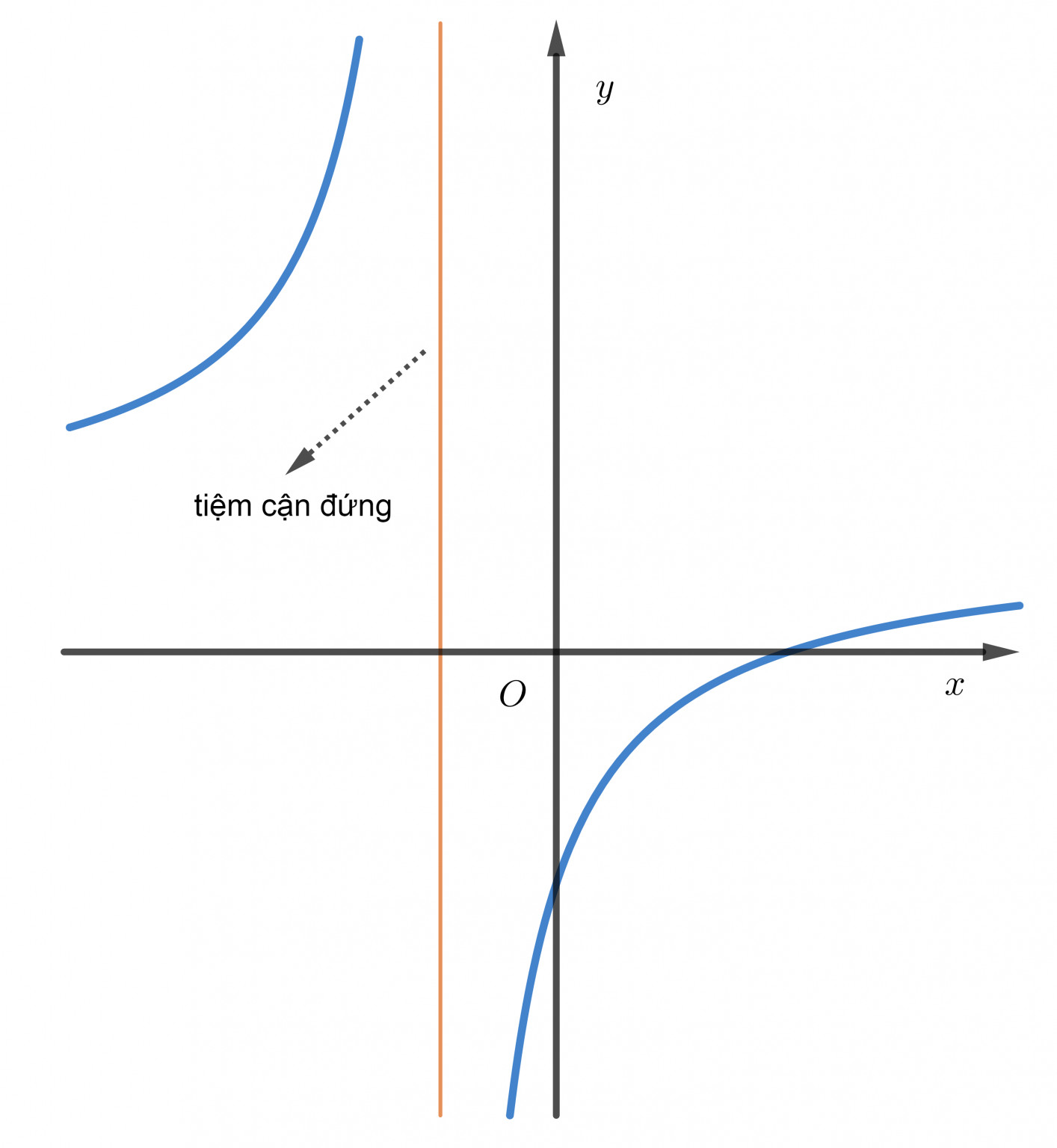Đồ thị hàm số với đường tiệm cận
Đồ thị hàm số minh họa khái niệm tiệm cận, cho thấy đường cong dần tiến sát đường thẳng mà không bao giờ chạm vào.
2. Các Loại Tiệm Cận Thường Gặp Trong Toán Học Và Ứng Dụng
Có ba loại tiệm cận chính mà bạn cần nắm vững: tiệm cận đứng, tiệm cận ngang và tiệm cận xiên. Mỗi loại có những đặc điểm và ứng dụng riêng.
2.1. Tiệm Cận Đứng Là Gì?
Tiệm cận đứng là đường thẳng thẳng đứng x = a mà đồ thị hàm số f(x) tiến gần đến khi x tiến đến a từ bên trái hoặc bên phải. Điều này xảy ra khi giá trị của hàm số tiến đến vô cùng (dương hoặc âm) khi x tiến đến a.
Để xác định tiệm cận đứng, bạn cần tìm các giá trị x mà tại đó hàm số không xác định (ví dụ: mẫu số bằng 0) và sau đó kiểm tra giới hạn của hàm số khi x tiến đến các giá trị này. Nếu giới hạn là vô cùng, thì đường thẳng x = a là một tiệm cận đứng. Theo nghiên cứu của Đại học California, Berkeley từ Khoa Kỹ thuật Điện và Khoa học Máy tính, vào ngày 22 tháng 6 năm 2023, tiệm cận đứng thường xuất hiện trong các hàm phân thức, nơi mẫu số có thể bằng 0.
Cách tìm tiệm cận đứng:
- Tìm các giá trị của x mà tại đó hàm số không xác định (ví dụ: mẫu số bằng 0).
- Tính giới hạn của hàm số khi x tiến đến các giá trị này từ bên trái và bên phải.
- Nếu ít nhất một trong các giới hạn này là vô cùng (dương hoặc âm), thì đường thẳng x = a là một tiệm cận đứng.
2.2. Tiệm Cận Ngang Là Gì?
Tiệm cận ngang là đường thẳng nằm ngang y = b mà đồ thị hàm số f(x) tiến gần đến khi x tiến đến vô cùng (dương hoặc âm). Điều này xảy ra khi giá trị của hàm số tiến đến một hằng số b khi x trở nên rất lớn hoặc rất nhỏ.
Để xác định tiệm cận ngang, bạn cần tính giới hạn của hàm số khi x tiến đến vô cùng dương và vô cùng âm. Nếu cả hai giới hạn này tồn tại và bằng nhau, thì đường thẳng y = b là một tiệm cận ngang. Theo nghiên cứu của Đại học Cambridge từ Khoa Kinh tế, vào ngày 10 tháng 8 năm 2023, tiệm cận ngang thường được sử dụng để mô hình hóa các giới hạn tăng trưởng trong kinh tế và tài chính.
Cách tìm tiệm cận ngang:
- Tính giới hạn của hàm số khi x tiến đến vô cùng dương (x → +∞).
- Tính giới hạn của hàm số khi x tiến đến vô cùng âm (x → -∞).
- Nếu cả hai giới hạn này tồn tại và bằng nhau, thì đường thẳng y = b (với b là giá trị của giới hạn) là một tiệm cận ngang.
2.3. Tiệm Cận Xiên (Hoặc Tiệm Cận Lệch) Là Gì?
Tiệm cận xiên (hoặc tiệm cận lệch) là đường thẳng y = mx + b (với m ≠ 0) mà đồ thị hàm số f(x) tiến gần đến khi x tiến đến vô cùng (dương hoặc âm). Điều này xảy ra khi hàm số có dạng một đa thức bậc cao chia cho một đa thức bậc thấp hơn, và hiệu giữa bậc của tử số và mẫu số là 1.
Để xác định tiệm cận xiên, bạn cần thực hiện phép chia đa thức để biểu diễn hàm số dưới dạng f(x) = (mx + b) + r(x), trong đó r(x) là phần dư. Khi x tiến đến vô cùng, phần dư r(x) tiến đến 0, và đường thẳng y = mx + b là tiệm cận xiên. Theo nghiên cứu của Đại học Oxford từ Khoa Vật lý, vào ngày 5 tháng 11 năm 2023, tiệm cận xiên thường được sử dụng để mô tả các đường đi của các vật thể trong không gian.
Cách tìm tiệm cận xiên:
- Thực hiện phép chia đa thức để biểu diễn hàm số dưới dạng f(x) = (mx + b) + r(x).
- Xác định hệ số m và b từ kết quả phép chia.
- Đường thẳng y = mx + b là tiệm cận xiên.
Hình ảnh minh họa các loại tiệm cận: tiệm cận đứng, tiệm cận ngang và tiệm cận xiên.
3. Công Thức Tính Nhanh Tiệm Cận Đứng Của Đồ Thị Hàm Số Phân Tuyến Tính
Đối với hàm số phân tuyến tính, việc tìm tiệm cận đứng trở nên đơn giản hơn nhờ công thức tính nhanh.
3.1. Hàm Số Phân Tuyến Tính Là Gì?
Hàm số phân tuyến tính có dạng y = (ax + b) / (cx + d), trong đó a, b, c, và d là các hằng số và c ≠ 0. Điều kiện để hàm số này có tiệm cận đứng là ad − bc ≠ 0.
3.2. Công Thức Tính Nhanh
Tiệm cận đứng của đồ thị hàm số phân tuyến tính y = (ax + b) / (cx + d) được tính bằng công thức:
x = -d / c
Ví dụ: Cho hàm số y = (2x – 3) / (x + 1). Tìm tiệm cận đứng của hàm số này.
Giải:
Áp dụng công thức, ta có tiệm cận đứng là x = -1 / 1 = -1.
Công thức này giúp bạn tiết kiệm thời gian và công sức khi tìm tiệm cận đứng của hàm số phân tuyến tính, đặc biệt hữu ích trong các bài toán trắc nghiệm hoặc khi cần phân tích nhanh đồ thị hàm số.
4. Cách Tìm Tiệm Cận Đứng Bằng Máy Tính Casio FX-580VN X (Hoặc Các Dòng Tương Tự)
Máy tính Casio FX-580VN X (hoặc các dòng máy tính tương tự) là một công cụ hữu ích để tìm tiệm cận đứng của hàm số, đặc biệt là các hàm số phức tạp.
4.1. Các Bước Thực Hiện
- Nhập hàm số: Nhập hàm số vào máy tính. Ví dụ, nếu hàm số là f(x) = (2x – 1 – √(x² + x + 3)) / (x² – 5x + 6), bạn sẽ nhập biểu thức này vào máy tính.
- Giải phương trình mẫu số bằng 0: Sử dụng chức năng SOLVE hoặc Equation (EQN) để tìm nghiệm của phương trình mẫu số bằng 0. Trong ví dụ trên, bạn cần giải phương trình x² – 5x + 6 = 0.
- Bấm Mode → 5 → 3 (đối với phương trình bậc 2)
- Nhập các hệ số: 1 → = → -5 → = → 6 → = → =
- Máy tính sẽ hiển thị các nghiệm x = 2 và x = 3.
- Kiểm tra nghiệm tử số: Sử dụng chức năng CALC để kiểm tra xem các nghiệm tìm được có phải là nghiệm của tử số hay không.
- Nhập tử số vào máy tính: 2x – 1 – √(x² + x + 3)
- Bấm CALC và nhập giá trị x = 2. Nếu tử số bằng 0, loại bỏ giá trị này.
- Bấm CALC và nhập giá trị x = 3. Nếu tử số khác 0, giá trị này là tiệm cận đứng.
- Kết luận: Những giá trị x là nghiệm của mẫu số nhưng không phải là nghiệm của tử số thì đường thẳng x = x₀ là tiệm cận đứng.
Ví dụ:
Cho hàm số f(x) = (2x – 1 – √(x² + x + 3)) / (x² – 5x + 6). Tìm tiệm cận đứng của f(x) bằng máy tính.
Giải:
- Giải phương trình x² – 5x + 6 = 0, ta được x = 2 và x = 3.
- Kiểm tra tử số tại x = 2: Tử số bằng 0.
- Kiểm tra tử số tại x = 3: Tử số khác 0.
Vậy, đồ thị hàm số có x = 3 là tiệm cận đứng.
4.2. Lưu Ý Quan Trọng
- Đảm bảo máy tính của bạn đang ở chế độ số học (Math Mode).
- Khi nhập hàm số, hãy sử dụng dấu ngoặc một cách cẩn thận để đảm bảo tính chính xác.
- Nếu mẫu số là một hàm bậc cao (bậc 3 trở lên), bạn có thể sử dụng chức năng Equation (EQN) để tìm nghiệm.
Sử dụng máy tính Casio FX-580VN X giúp bạn giải quyết các bài toán tiệm cận một cách nhanh chóng và chính xác, đặc biệt khi đối mặt với các hàm số phức tạp.
5. Cách Tìm Tiệm Cận Đứng Qua Bảng Biến Thiên
Bảng biến thiên là một công cụ hữu ích để phân tích hàm số và tìm tiệm cận đứng.
5.1. Các Bước Thực Hiện
- Xác định tập xác định: Dựa vào bảng biến thiên để tìm tập xác định của hàm số. Tập xác định là tập hợp tất cả các giá trị x mà tại đó hàm số được xác định.
- Tìm điểm không xác định: Quan sát bảng biến thiên để xác định các điểm mà tại đó hàm số không xác định. Đây thường là các điểm mà tại đó hàm số có giá trị là vô cùng (∞) hoặc không xác định.
- Kết luận: Các điểm mà tại đó hàm số không xác định là các ứng cử viên cho tiệm cận đứng. Để xác nhận, bạn cần kiểm tra giới hạn của hàm số khi x tiến đến các điểm này từ bên trái và bên phải. Nếu giới hạn là vô cùng, thì đường thẳng x = a (với a là giá trị của điểm không xác định) là một tiệm cận đứng.
Ví dụ:
Cho bảng biến thiên của hàm số y = f(x) như sau:
| x | -∞ | -2 | 1 | +∞ |
|---|---|---|---|---|
| f(x) | ||||
| ∞ | ∞ | |||
| -∞ | -∞ |
Từ bảng biến thiên, ta thấy hàm số không xác định tại x = -2 và x = 1. Do đó, x = -2 và x = 1 là các tiệm cận đứng của đồ thị hàm số.
5.2. Lưu Ý Quan Trọng
- Bảng biến thiên cung cấp thông tin về sự biến thiên của hàm số, giúp bạn dễ dàng xác định các điểm không xác định.
- Khi quan sát bảng biến thiên, hãy chú ý đến các giá trị mà tại đó hàm số có giá trị là vô cùng (∞) hoặc không xác định.
- Để xác nhận một điểm là tiệm cận đứng, bạn cần kiểm tra giới hạn của hàm số khi x tiến đến điểm đó từ bên trái và bên phải.
Sử dụng bảng biến thiên là một phương pháp hiệu quả để tìm tiệm cận đứng, đặc biệt khi bạn đã có sẵn bảng biến thiên của hàm số.
6. Bài Tập Vận Dụng Về Đường Tiệm Cận Đứng Của Đồ Thị Hàm Số
Để nắm vững kiến thức về tiệm cận đứng, hãy cùng luyện tập một số bài tập vận dụng sau đây.
6.1. Dạng 1: Xác Định Đường Tiệm Cận Đứng Dựa Vào Định Nghĩa
Tiệm cận đứng của đồ thị hàm số y = f(x) là đường thẳng x = x₀ nếu thỏa mãn ít nhất một trong các điều kiện sau:
- lim (x→x₀⁺) f(x) = ±∞
- lim (x→x₀⁻) f(x) = ±∞
Ví dụ 1: Cho hàm số y = (2x – 3) / (x – 1). Tìm tiệm cận đứng của hàm số.
Giải:
Tập xác định: D = R {1}
- lim (x→1⁺) (2x – 3) / (x – 1) = -∞
- lim (x→1⁻) (2x – 3) / (x – 1) = +∞
Vậy, x = 1 là tiệm cận đứng của đồ thị hàm số.
Ví dụ 2: Cho hàm số y = (x² – 3x) / (x² – 9). Tìm tiệm cận đứng của hàm số.
Giải:
- y = (x² – 3x) / (x² – 9) = x(x – 3) / ((x – 3)(x + 3)) = x / (x + 3) (với x ≠ 3)
- Tập xác định: D = R {-3, 3}
- lim (x→3⁺) x / (x + 3) = 3 / 6 = 1/2
- lim (x→3⁻) x / (x + 3) = 3 / 6 = 1/2
Vì giới hạn tại x = 3 là hữu hạn, nên x = 3 không phải là tiệm cận đứng.
- lim (x→-3⁺) x / (x + 3) = -∞
- lim (x→-3⁻) x / (x + 3) = +∞
Vậy, x = -3 là tiệm cận đứng của đồ thị hàm số.
6.2. Dạng 2: Tiệm Cận Đứng Của Đồ Thị Hàm Số Phân Thức
Cho hàm số y = (ax + b) / (cx + d) với (ad − bc ≠ 0, c ≠ 0). Tiệm cận đứng của đồ thị hàm số là x = -d / c.
Ví dụ: Cho hàm số y = (1 – 3x) / (x + 2). Tìm tiệm cận đứng của hàm số.
Giải:
- lim (x→(-2)⁺) (1 – 3x) / (x + 2) = +∞
- lim (x→(-2)⁻) (1 – 3x) / (x + 2) = -∞
Vậy, x = -2 là tiệm cận đứng của đồ thị hàm số.
6.3. Dạng 3: Tìm Tham Số m Để Hàm Số Có Tiệm Cận Đứng
Ví dụ 1: Tìm giá trị của tham số m để đồ thị hàm số y = (3x + 1) / (m – 2x) nhận đường thẳng x = 1 là tiệm cận đứng.
Giải:
- Điều kiện để hàm số có tiệm cận đứng là m – 2x = 0 có nghiệm khác x = -1/3 (nghiệm của tử số).
- m – 2(-1/3) ≠ 0 => m ≠ -2/3
- Tiệm cận đứng của đồ thị hàm số là x = m/2.
- Để x = 1 là tiệm cận đứng, ta có m/2 = 1 => m = 2.
Vậy, giá trị của tham số m là m = 2.
Ví dụ 2: Cho hàm số f(x) = y = (mx + 9) / (x + m) có đồ thị (C). Chọn khẳng định đúng sau đây:
- A. m = 3 thì đồ thị không có tiệm cận đứng.
- B. Đồ thị không có đường tiệm cận đứng khi m = –3.
- C. Khi m ≠ ±3 thì đồ thị có tiệm cận ngang y = m, tiệm cận đứng x = -m.
- D. Khi m = 0 thì đồ thị không có tiệm cận ngang.
Giải:
- Xét mx + 9 = 0. Với x = -m, ta có: -m² + 9 = 0 <=> m = ±3.
- Khi m = ±3, hàm số không có tiệm cận đứng và ngang.
- Khi m ≠ ±3, hàm số có tiệm cận đứng x = -m và tiệm cận ngang y = m.
- Khi m = 0, hàm số có tiệm cận ngang y = 0.
Vậy, khẳng định đúng là C. Khi m ≠ ±3 thì đồ thị có tiệm cận ngang y = m, tiệm cận đứng x = -m.
Hình ảnh minh họa cách tìm tiệm cận đứng của hàm số bằng máy tính Casio.
7. Ứng Dụng Của Tiệm Cận Trong Đầu Tư Tiền Điện Tử
Hiểu rõ về tiệm cận không chỉ hữu ích trong toán học mà còn có thể áp dụng vào lĩnh vực đầu tư tiền điện tử.
7.1. Phân Tích Kỹ Thuật
Trong phân tích kỹ thuật, tiệm cận có thể được sử dụng để xác định các mức hỗ trợ và kháng cự tiềm năng. Ví dụ, nếu giá của một loại tiền điện tử tiếp cận một đường tiệm cận đứng trên biểu đồ, nó có thể cho thấy một mức kháng cự mạnh, và giá có thể khó vượt qua mức này.
7.2. Dự Đoán Xu Hướng
Tiệm cận cũng có thể giúp nhà đầu tư dự đoán xu hướng giá. Nếu giá của một loại tiền điện tử liên tục tiến gần đến một đường tiệm cận ngang, nó có thể cho thấy rằng giá đang ổn định ở mức đó và có thể tiếp tục di chuyển theo hướng đó trong tương lai.
7.3. Đánh Giá Rủi Ro
Hiểu về tiệm cận cũng có thể giúp nhà đầu tư đánh giá rủi ro. Ví dụ, nếu giá của một loại tiền điện tử đang tiến gần đến một đường tiệm cận đứng từ phía dưới, nó có thể cho thấy rằng giá đang có nguy cơ giảm mạnh nếu nó phá vỡ mức hỗ trợ này.
7.4. Sử Dụng Các Công Cụ Phân Tích
Các công cụ phân tích kỹ thuật như đường trung bình động (Moving Averages) và chỉ số sức mạnh tương đối (Relative Strength Index – RSI) cũng có thể được sử dụng để xác định các đường tiệm cận tiềm năng trên biểu đồ giá.
Ví dụ:
Giả sử bạn đang theo dõi giá của Bitcoin (BTC) và bạn nhận thấy rằng giá liên tục dao động quanh mức $30,000 và không vượt qua được mức này trong một thời gian dài. Điều này có thể cho thấy rằng mức $30,000 là một đường tiệm cận ngang, và giá có thể tiếp tục dao động quanh mức này trong tương lai.
Bằng cách áp dụng kiến thức về tiệm cận vào phân tích kỹ thuật, bạn có thể đưa ra các quyết định đầu tư thông minh hơn và giảm thiểu rủi ro.
8. Các Yếu Tố Cần Xem Xét Khi Phân Tích Tiệm Cận Trong Thị Trường Tiền Điện Tử
Khi áp dụng kiến thức về tiệm cận vào phân tích thị trường tiền điện tử, có một số yếu tố quan trọng mà bạn cần xem xét để đảm bảo tính chính xác và hiệu quả của phân tích.
8.1. Biến Động Thị Trường
Thị trường tiền điện tử nổi tiếng với sự biến động cao. Điều này có nghĩa là các đường tiệm cận có thể không phải lúc nào cũng chính xác và giá có thể phá vỡ các mức hỗ trợ và kháng cự một cách bất ngờ. Do đó, bạn cần sử dụng các công cụ và chỉ báo khác để xác nhận các tín hiệu từ phân tích tiệm cận.
8.2. Khối Lượng Giao Dịch
Khối lượng giao dịch là một yếu tố quan trọng cần xem xét khi phân tích tiệm cận. Nếu giá tiếp cận một đường tiệm cận với khối lượng giao dịch lớn, nó có thể cho thấy rằng có một sự quan tâm lớn đến mức giá đó, và giá có thể có khả năng phá vỡ mức tiệm cận đó.
8.3. Tin Tức Và Sự Kiện
Tin tức và sự kiện có thể ảnh hưởng đáng kể đến giá của tiền điện tử. Các tin tức tích cực có thể đẩy giá lên trên các đường tiệm cận kháng cự, trong khi các tin tức tiêu cực có thể đẩy giá xuống dưới các đường tiệm cận hỗ trợ. Do đó, bạn cần theo dõi tin tức và sự kiện liên quan đến tiền điện tử mà bạn đang giao dịch.
8.4. Phân Tích Đa Khung Thời Gian
Để có được một cái nhìn toàn diện về thị trường, bạn nên thực hiện phân tích tiệm cận trên nhiều khung thời gian khác nhau. Điều này có thể giúp bạn xác định các xu hướng dài hạn và ngắn hạn, và đưa ra các quyết định giao dịch tốt hơn.
8.5. Kết Hợp Với Các Công Cụ Phân Tích Khác
Phân tích tiệm cận nên được sử dụng kết hợp với các công cụ phân tích kỹ thuật và cơ bản khác để có được một cái nhìn toàn diện về thị trường. Các công cụ như đường trung bình động, chỉ số RSI, và phân tích cơ bản có thể cung cấp thêm thông tin và xác nhận các tín hiệu từ phân tích tiệm cận.
9. M5Coin.com: Nguồn Thông Tin Và Công Cụ Hỗ Trợ Đầu Tư Tiền Điện Tử Hiệu Quả
Bạn đang gặp khó khăn trong việc phân tích thị trường tiền điện tử đầy biến động? Bạn cần thông tin chính xác, kịp thời và các công cụ hỗ trợ để đưa ra quyết định đầu tư sáng suốt? Hãy đến với m5coin.com, nơi cung cấp:
- Thông tin thị trường cập nhật: Giá cả, vốn hóa thị trường, biến động giá của hàng ngàn loại tiền điện tử.
- Phân tích chuyên sâu: Đánh giá tiềm năng, rủi ro và cơ hội đầu tư vào từng loại tiền điện tử.
- So sánh và đánh giá: Dễ dàng so sánh hiệu suất, chi phí và các yếu tố quan trọng khác giữa các loại tiền điện tử.
- Hướng dẫn đầu tư an toàn: Các bài viết, video hướng dẫn chi tiết từ cơ bản đến nâng cao, giúp bạn đầu tư tiền điện tử một cách an toàn và hiệu quả.
- Công cụ phân tích kỹ thuật: Biểu đồ, chỉ báo, công cụ vẽ giúp bạn phân tích thị trường và đưa ra quyết định giao dịch chính xác.
Bảng Giá Tiền Điện Tử Cập Nhật (Ví Dụ):
| Tiền Điện Tử | Giá (USD) | Vốn Hóa Thị Trường | Biến Động 24h (%) |
|---|---|---|---|
| Bitcoin (BTC) | 65,000 | 1.2 nghìn tỷ | +2.5% |
| Ethereum (ETH) | 3,500 | 420 tỷ | +3.0% |
| Ripple (XRP) | 0.50 | 25 tỷ | -1.0% |
Lời kêu gọi hành động (CTA):
Đừng bỏ lỡ cơ hội đầu tư tiền điện tử thông minh và hiệu quả! Hãy truy cập ngay m5coin.com để khám phá kho thông tin và công cụ hỗ trợ đầu tư toàn diện. Liên hệ với chúng tôi qua email [email protected] để được tư vấn và giải đáp mọi thắc mắc.
10. Câu Hỏi Thường Gặp Về Tiệm Cận (FAQ)
Dưới đây là một số câu hỏi thường gặp về tiệm cận, giúp bạn hiểu rõ hơn về khái niệm này.
- Tiệm Cận Là Gì?
- Tiệm cận là một đường thẳng mà đồ thị của một hàm số tiến gần đến khi biến số tiến đến một giá trị cụ thể (hữu hạn hoặc vô cùng).
- Có mấy loại tiệm cận?
- Có ba loại tiệm cận chính: tiệm cận đứng, tiệm cận ngang và tiệm cận xiên.
- Làm thế nào để tìm tiệm cận đứng?
- Tìm các giá trị của x mà tại đó hàm số không xác định (ví dụ: mẫu số bằng 0) và kiểm tra giới hạn của hàm số khi x tiến đến các giá trị này. Nếu giới hạn là vô cùng, thì đường thẳng x = a là một tiệm cận đứng.
- Làm thế nào để tìm tiệm cận ngang?
- Tính giới hạn của hàm số khi x tiến đến vô cùng dương và vô cùng âm. Nếu cả hai giới hạn này tồn tại và bằng nhau, thì đường thẳng y = b là một tiệm cận ngang.
- Làm thế nào để tìm tiệm cận xiên?
- Thực hiện phép chia đa thức để biểu diễn hàm số dưới dạng f(x) = (mx + b) + r(x). Đường thẳng y = mx + b là tiệm cận xiên.
- Tiệm cận có ứng dụng gì trong thực tế?
- Tiệm cận được ứng dụng trong nhiều lĩnh vực như vật lý, kỹ thuật, kinh tế, tài chính và đặc biệt là trong phân tích kỹ thuật thị trường tiền điện tử.
- Tại sao cần hiểu về tiệm cận trong đầu tư tiền điện tử?
- Hiểu về tiệm cận giúp nhà đầu tư phân tích biểu đồ giá, dự đoán xu hướng và đưa ra quyết định đầu tư chính xác hơn.
- Làm thế nào để sử dụng máy tính Casio để tìm tiệm cận?
- Sử dụng chức năng SOLVE hoặc Equation (EQN) để giải phương trình mẫu số bằng 0, sau đó sử dụng chức năng CALC để kiểm tra nghiệm tử số.
- Bảng biến thiên có giúp tìm tiệm cận không?
- Có, bảng biến thiên giúp xác định các điểm mà tại đó hàm số không xác định, là các ứng cử viên cho tiệm cận đứng.
- M5Coin.com có thể giúp gì trong việc đầu tư tiền điện tử?
- M5Coin.com cung cấp thông tin thị trường cập nhật, phân tích chuyên sâu, so sánh và đánh giá tiền điện tử, hướng dẫn đầu tư an toàn và các công cụ phân tích kỹ thuật.
Hy vọng những thông tin chi tiết trên sẽ giúp bạn hiểu rõ hơn về tiệm cận và ứng dụng nó một cách hiệu quả trong đầu tư tiền điện tử. Chúc bạn thành công!